知ってる人には当然だろうけど、知らないと「なるほどね」になるやつ。
自分は、モンテカルロ法を勉強した後に寝ていたら思いついて、自分のことを天才かと疑いました(既出)
モンテカルロ法とは
乱択アルゴリズムの一つです。
雑にとらえる
標本空間$\Omega$について、$\Omega = \{ a, b, c, …, z \}$とします。
これから$N$回の試行を行い、各試行では、$\Omega$の要素$X$を一つ得ます。各試行は独立で、一回前の試行で出た要素が今回の試行では出ないというようなことはありません。
ここで、任意の$X \in \Omega$について、$X$の出やすさ$P(X)$が定まっているとします。
あなたは、$P(X)$の値を知りません。そこで、すべての$X \in \Omega$について$P(X)$が知りたくなりました。すべての$X \in \Omega$について、$P(X)$を予想してください。
$N$回の試行のうち、$X \in \Omega$が出た回数を$C(X)$とおいてみます。
このとき、$P(X) = \dfrac{C(X)}{N}$であると予想できます。また、$N$が大きくなれば大きくなるほど、$P(X)$はより正しい値に近づくことも予想できます。(大数の法則)
モンテカルロ法は、この確率の基本的な考え方を用いて、シミュレーションや数値計算を乱数を用いて行おうという手法のことです。
積分
モンテカルロ法のチュートリアルみたいな問題によく出てくるものとして、円周率を求めるものがあります。アルゴリズムは以下の通りです。
- $0.0 \le x, y \le 1.0$として、$x, y$の組を$N$組、ランダムに生成する。このとき、できるだけ一様な乱数を選ぶ。
- $N$個の組について、$x^2 + y^2 <= 1$である組の個数を調べる。このとき条件を満たす$(x, y)$の個数を$C$を置く。
- $4\dfrac{C}{N}$が円周率となる。
これを単純に$y = \sqrt{1-x^2}$の$x \ge 0$部分1と、$y = 0, x = 0$で囲まれる部分の面積の積分と捉えることができます。
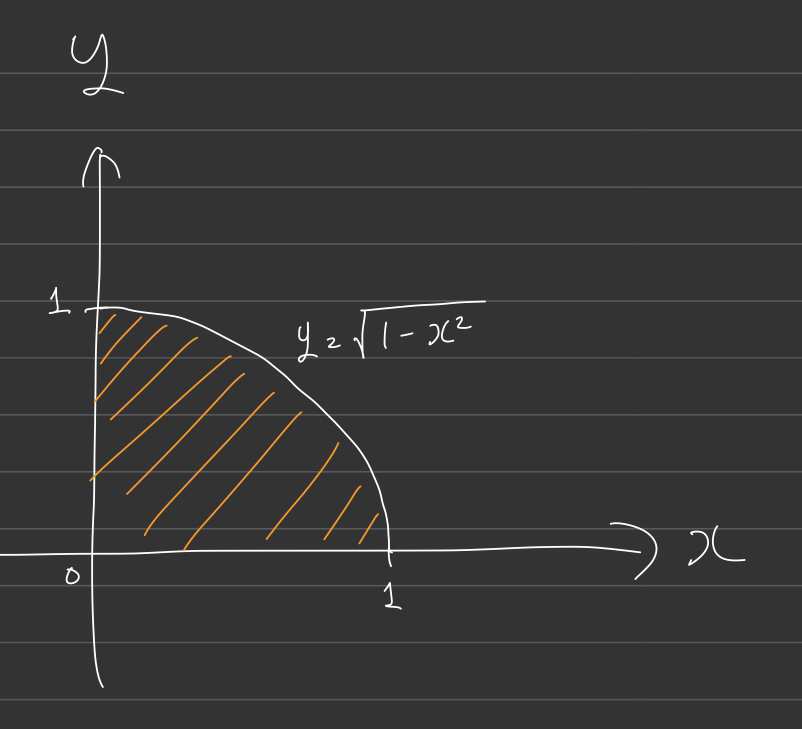
すなわち、
$ \dfrac{C}{N} \simeq \int_{0}^{1}{\sqrt{1-x^2}}\hspace{0.25em}dx $
です。
実際、$\int_{0}^{1}{\sqrt{1-x^2}}\hspace{0.25em}dx \simeq 0.785398163397$であり、$4 \times 0.785398163397 \simeq \pi$です。
一般化しよう
区間$[a, b]$で定義される、正の実数を返す関数$f(x)$について、区間内の最大値を$M$と書くことにします。
このとき、$y = 0, x = a, x = b$と$f(x)$によって囲まれる領域の面積$S$は
$ S = \int_{a}^{b}{f(x)} $
です。
モンテカルロ法で円周率を求める方法を参考にして、以下の試行を$N$回行います。このとき、$N$には十分大きい値を選びましょう。
- $a \le x \le b$、$0 \le y \le M$として、$N$個の$(x, y)$の組をランダムに生成する。このとき、できるだけ一様な乱数を選ぶ。
- $N$個の組について、$y <= f(x)$である組の個数を調べる。このとき条件を満たす$(x, y)$の個数を$C$を置く。
- $M(b-a)\dfrac{C}{N}$が$S$の近似値となる。
やってみよう
$ \int_{5}^{20}{\dfrac{1}{x}} dx = \log{20} - \log{5} = \log{4} \simeq = 1.38629\dots $
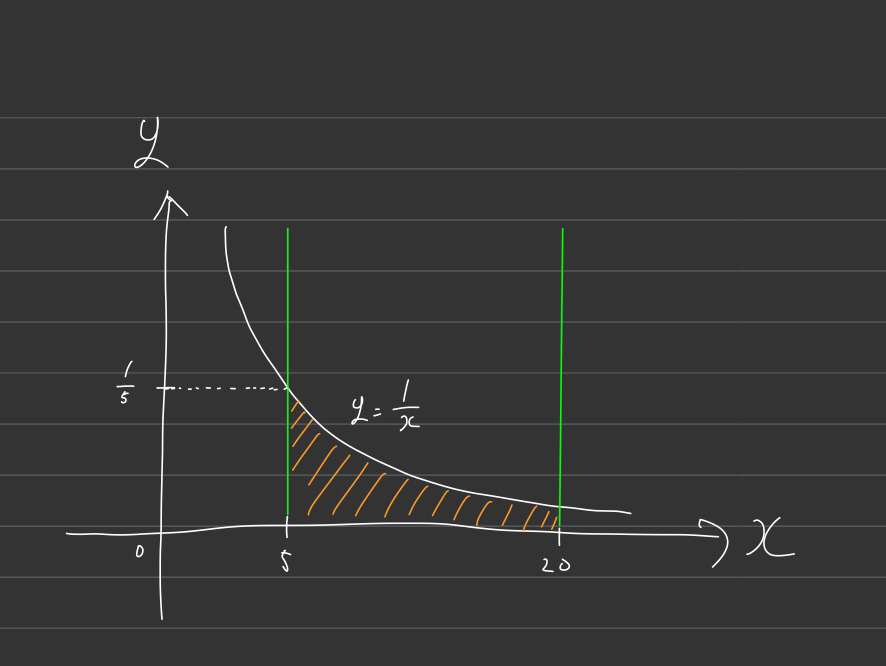
を求めます。
import numpy as np
import math as m
a, b = 5, 20
M = 1/a
n = 10000000
x = np.random.random(n)*(b-a)
x = x + a
y = np.random.random(n)*M
C = 0
for xi, yi in zip(x, y):
if yi <= (1/xi):
C += 1
print(M*(b-a)*(C/n))
こんな感じのコードを書きます。
5回程度実行して結果を見てみます。
| 回数 | 結果 |
|---|---|
| 1 | 1.3862022 |
| 2 | 1.3861029 |
| 3 | 1.3859157 |
| 4 | 1.3856925 |
| 5 | 1.3861752 |
実行回数が少ないのでなんとも言えないですが、まあまあいい精度で計算できていると思います。
原理
原理は単純で、区間の面積を長方形として見て、どれくらいの割合が関数に含まれているかを調べているだけです。
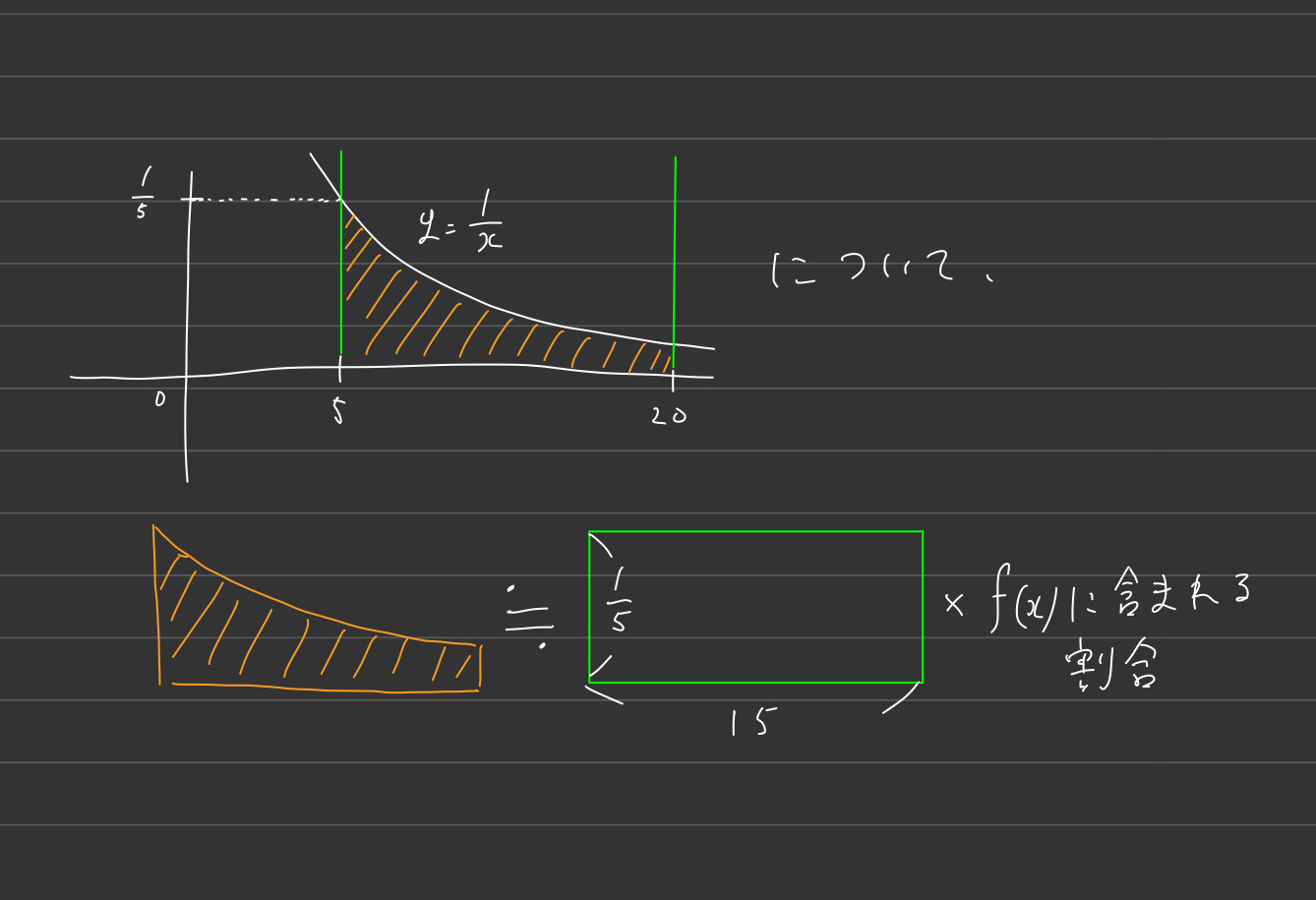
拡張
聡明な読者諸君はお気づきのことだろうと思いますが、別に$y = f(x)$の形の関数でなくても良いです。$c = f(a, b)$や$d = f(a, b, c)$のような関数でも、当然求めることができます。
つまり、$2$より大きな次元について、この方法を用いることができます。
例えば、半径が$r$である球は$r^2 = x^2 + y^2 + z^2$として表されます。この球の体積を求めたいです。
例によって、円のときのモンテカルロ法を思い出すと、以下のようなアルゴリズムを得ます。
- $0.0 \le x, y, z \le r$として、$x, y, z$の組を$N$組、ランダムに生成する。このとき、できるだけ一様な乱数を選ぶ。
- $N$個の組について、$x^2 + y^2 + z^2 <= r^2$である組の個数を調べる。このとき条件を満たす$(x, y, z)$の個数を$C$を置く。
- $(2r)^3\dfrac{C}{N}$が体積となる。
ここで、$r = 3$の球の体積$V$は、
$ \begin{aligned} V &= \int_{-r}^{r}{\pi (\sqrt{r^2 - x^2})^2} dx \\ &= 2\pi \int_{0}^{r}{(r^2-x^2)} dx \\ &= \dfrac{4}{3}\pi r^3 \\ \end{aligned} $
より、$V = 27\frac{4}{3}\pi \simeq 113.09733552923$です。
import numpy as np
import math as m
r = 3
n = 1000000
x = np.random.random(n)*r
y = np.random.random(n)*r
z = np.random.random(n)*r
C = 0
for xi, yi, zi in zip(x, y, z):
if xi**2 + yi**2 + zi**2 <= r**2:
C += 1
print(((2*r)**3)*(C/n))
今回はこんなコードを書きます。
同様に5回程度実行して結果を見ます。($n = 10^6$)
| 回数 | 結果 |
|---|---|
| 1 | 113.07578400000001 |
| 2 | 113.19263999999998 |
| 3 | 113.07751199999998 |
| 4 | 113.026104 |
| 5 | 113.08248 |
こちらも、多少ブレはありますが、まあ許容できる範囲の誤差だと思います。誤差を減らしたいなら、単純にnを増やせば良いです。
| n | 10回の平均 | 誤差 ($|113.09733552923 - \text{平均値}|$) |
|---|---|---|
| $10^2$ | 110.16000000000001 | 2.9373355292299834 |
| $10^3$ | 111.99600000000001 | 1.101335529229985 |
| $10^4$ | 113.48856 | 0.39122447077001254 |
| $10^5$ | 113.203656 | 0.10632047077000095 |
| $10^6$ | 113.0994144 | 0.018019670770030416 |
| $10^7$ | 113.11433568000002 | 0.017000150770030587 |
$n \ge 10^8$については、時間がかかるので勘弁してください。
おわり
うまぴょい
ところで、この方法、$n$次ユークリッド空間の超球などについては適用できそうですが、$n$次元空間内で歪な形をした関数の場合どうなるんでしょう?
参考文献
- モンテカルロ法 - Wikipedia
- 確率変数 - Wikipedia
- n次元超球の体積の求め方と考察 | 高校数学の美しい物語
- 球面の方程式に関する5つの公式と具体例 | 高校数学の美しい物語
- 球の体積と表面積の公式の覚え方・積分での求め方 | 高校数学の美しい物語
-
これをいい感じにやる式が思いつかなかったんですが、なにかあったりしないんですか? ↩