座標平面上で点を回します
解きたい問題
AtCoder Beginner Contest 197: D - Opposite
$x, y$座標平面上に正$\hspace{0.15em}N$角形があり、$N$個の頂点は反時計回りに$\hspace{0.15em}p_{0}, \hspace{0.15em}p_{1},\hspace{0.15em} p_{2},\hspace{0.15em} …, \hspace{0.15em}p_{N-1}$と番号がついている。
ここで$\hspace{0.15em}N$は偶数である。
$p_{0}$と$\hspace{0.15em}p_{\frac{N}{2}}$の座標が与えられるので$\hspace{0.15em}p_{1}$の座標を求めよ。
(制約はリンク先参照)
方針
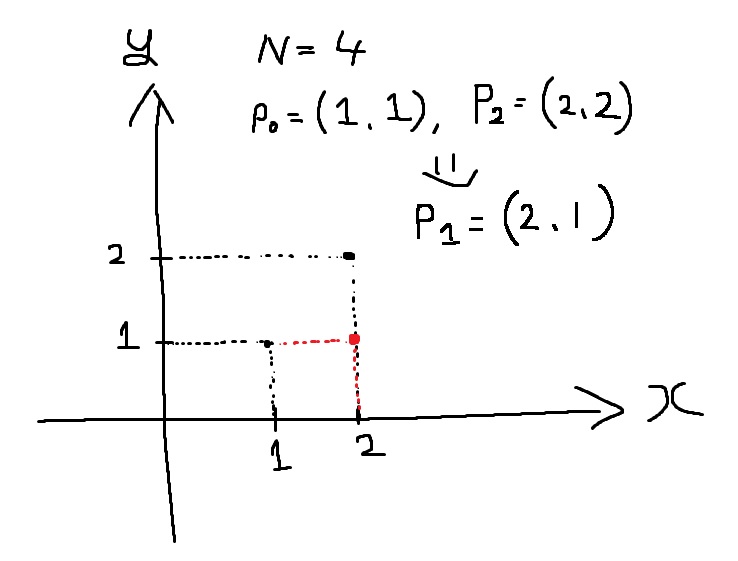
適当にサンプル1を見てみると、この時点でやりたいことは大体わかります。
正$\hspace{0.15em}N$角形を$\theta = \dfrac{2\pi}{N}$だけ回転させると$\hspace{0.15em}p_{0}$が$\hspace{0.15em}p_{1}$に、$p_{\frac{N}{2}}$が$\hspace{0.15em}p_{\frac{N}{2}+1}$になります。
よって、正$N$角形を$\theta = \dfrac{2\pi}{N}$だけ回転させたときの点$\hspace{0.15em}p_{0}$の座標を知りたいです。
原点からの回転
これどうやら旧指導要領の数学2, Bでやるらしいです(そうなんですか?)
座標平面上の点 $\hspace{0.15em}P(a, b)$ と原点がなす線分 $\hspace{0.15em}\text{OP}\hspace{0.15em}$ を原点を軸として $\hspace{0.15em}\theta\hspace{0.15em}$ だけ回転させることを考えます。これは実質的に点 $\hspace{0.15em}P\hspace{0.15em}$ を $\hspace{0.15em}\theta\hspace{0.15em}$ だけ回転させることと同義です。
$x$ 軸と線分 $\text{OP}$ がなす角を $\alpha$ と置くと、
$\cos{\alpha} = \dfrac{a}{\text{OP}}, \hspace{0.5em} \sin{\alpha} = \dfrac{b}{\text{OP}}$
です。
回転したあとの点を$Q$と置くと、 $\sin , \cos$の定義より $Q(\text{OP}\cos{(\alpha + \theta)}, \text{OP}\sin{(\alpha + \theta)})$ です。
$\cos{(\alpha + \theta)}$ と $\sin{(\alpha + \theta)}$ を加法定理を用いて展開すると
$ \begin{aligned} \cos{(\alpha + \theta)} &= \cos{\alpha}\cos{\theta} - \sin{\alpha}\sin{\theta} \\ &= \dfrac{a}{\text{OP}} \cos{\theta} - \dfrac{b}{\text{OP}}\sin{\theta} \end{aligned} $
$ \begin{aligned} \sin{(\alpha + \theta)} &= \sin{\alpha}\cos{\theta} + \cos{\alpha}\sin{\theta} \\ &= \dfrac{b}{\text{OP}}\cos{\theta} + \dfrac{a}{\text{OP}}\sin{\theta} \end{aligned} $
を得ます。
ここで
$Q \left( \text{OP}\left( \dfrac{a}{\text{OP}}\cos{\theta} - \dfrac{b}{\text{OP}}\sin{\theta}\right) , \text{OP}\left( \dfrac{b}{\text{OP}}\cos{\theta} + \dfrac{a}{\text{OP}}\sin{\theta} \right) \right)$
です。
$x, y$成分ともに全ての項の分母分子が共通因数$\text{OP}$を持つので、$\text{OP} = 1$と読み替えてよいです。
したがって$Q(a\cos{\theta} - b\sin{\theta}, \hspace{0.2em} b\cos{\theta} + a\sin{\theta})$を得ます。
もとの問題
もともと考えていた問題では正$\hspace{0.15em}N\hspace{0.15em}$角形を$\theta$だけ回転させることを考えていました。
これは、正$\hspace{0.15em}N\hspace{0.15em}$角形の中心点を軸として座標平面を回転させることを意味します。
したがって、今ちょうど得たばかりの方法では多角形単体を回転させることができません。
これを解決するのは意外と簡単で、多角形の中心点が座標平面の原点となるように頂点を平行移動すれば良いです。\
もとの問題ではちょうど$\hspace{0.15em}p_{0}\hspace{0.15em}$と$\hspace{0.15em}p_{\frac{N}{2}}\hspace{0.15em}$が与えられていました。
この2つはちょうど対角線で結ばれる関係にあり、対角線の中点が多角形の中心となります。
中点は点$\hspace{0.15em}p_{0}\hspace{0.15em}$と$\hspace{0.15em}p_{\frac{N}{2}}\hspace{0.15em}$を$1:1$に内分する点です。
$i$番目の頂点の$x, y$座標をそれぞれ$\hspace{0.15em}xp_{i}, \hspace{0.15em}yp_{i}\hspace{0.15em}$と表すことにすると中点$H$は
$ H = \left(\dfrac{xp_{0} + xp_{\frac{N}{2}}}{2}, \dfrac{yp_{0} + yp_{\frac{N}{2}}}{2} \right) $
です。
ここまで来たら$xp_{1}, yp_{1}$から$x, y$成分を独立に中点の座標分だけひいてやると多角形の中心が原点となるように平行移動ができました。
平行移動したあとに回転移動を行い、元の位置に戻すように最初とは反対の平行移動をしてやると求める\(x, y\)座標を得ます。
提出 #31482169 - AtCoder Beginner Contest 197(Sponsored by Panasonic)
余談
今回は真面目に平行移動したり回転移動したりしましたが、中心点から$p_{0}$へ向かうベクトル$\boldsymbol{a}$を考えるとそのベクトルを$\dfrac{2\pi}{N}$だけ回転させればよいです。
幾何学ライブラリを持っている人ならそっちの方が楽だったりすると思います。